그래프

그래프 이론에서 그래프란: 객체의 일부 쌍들이 ‘연관되어’ 있는 객체 집합 구조

오일러의 경로

오일러의 경로

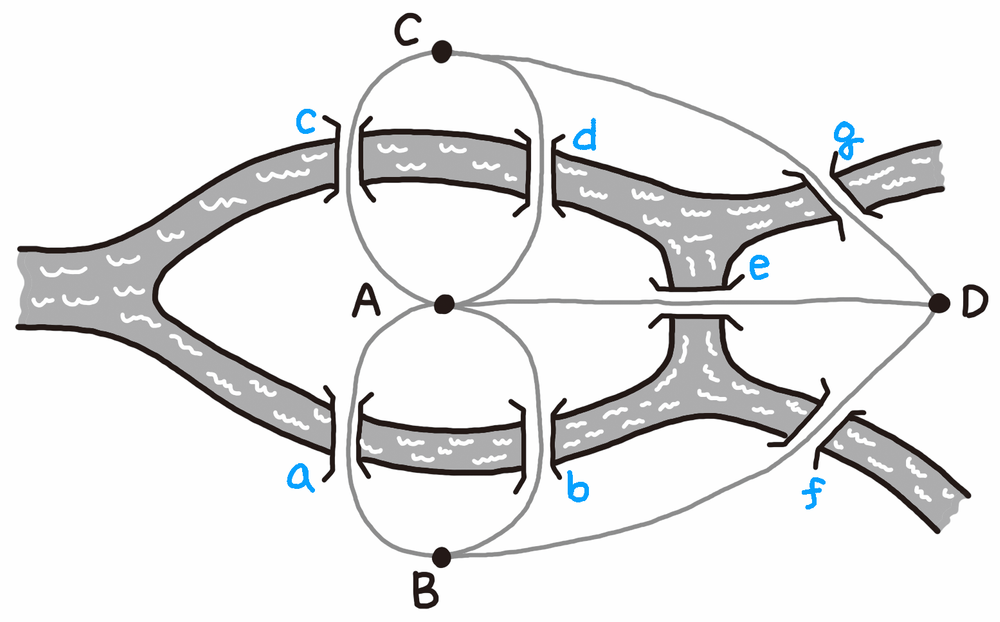
오일러의 정리: 모든 정점이 짝수 개의 차수를 갖는다면 모든 다리를 한 번씩만 건너서 도달할 수 있다.

오일러의 경로: 모든 간선(edge)을 한 번씩 방문하는 유한 그래프

해밀턴 경로

각 정점(vertex)을 한 번씩 방문하는 무항 또는 유향 그래프 경로

해밀턴 경로를 찾는 문제는 최적 알고리즘이 없는 대표적인 NP-완전 문제이다.

해밀턴 순환: 원래의 출발점으로 돌아오는 경로. 이 중에서도 특히 최단 거리를 찾는 문제는 외판원 문제로 유명하다.

NP 복잡도

NP: 비결정론적 튜링 기계(NTM)로 다항 시간 안에 풀 수 있는 판정 문제의 집합

P(결정론적 튜링 기계 문제) < NP

• 해밀턴 경로: 한 번만 방문하는 경로 (NP-완전 문제)
• 해밀턴 순환: 한 번만 방문하여 출발지로 돌아오는 경로 (NP-난해 문제)
• 외판원 문제: 한 번만 방문하여 출발지로 돌아오는 경로 중 가장 짧은 경로

NP-완전 문제의 조건: NP 문제이다 and NP-난해 문제이다

그래프 순회

그래프 순회란, 그래프 탐색이라고도 불리우며 그래프의 각 정점을 방문하는 과정이다.

그래프를 표현하는 방법

그래프

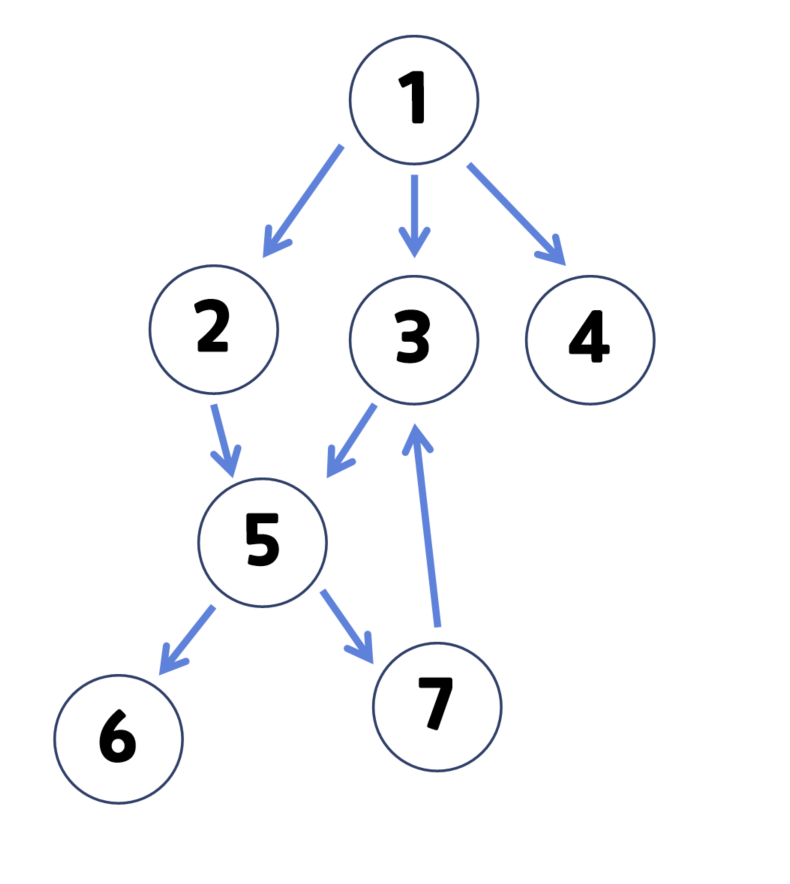
• 인접 행렬
• 인접 리스트: 출발 노드를 키로, 도착 노드를 값으로 하여 딕셔너리로 표현할 수 있다.
• graph = { 1 : [2,3,4], 2 : [5], 3 : [5], 4 : [], 5 : [6,7], 6 : [], 7 : [3] }

깊이 우선 탐색(DFS)

루트 노드에서 다음 branch로 넘어가기 전에 해당 branch를 완벽하게 탐색하는 방법

( 설명 출처: https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html )

일반적으로 많이 사용하는 알고리즘. 주로 스택이나 재귀로 구현.

백트래킹을 통해 뛰어난 효용을 보인다.

 

재귀 구조

• 재귀 구조로 구현

  # v: 정점
  
  def recursive_dfs(v, discovered=[]):
      discovered.append(v)
      for w in graph[v]:
          if w not in discovered:
              discovered = recursive_dfs(w, discovered)
      return discovered

• (코딩 테스트 시에도 재귀 구현이 더 선호되는 편)

 

스택 이용

• 스택을 이용한 반복 구조로 구현

  def iterative_dfs(start_v):
      discovered = []
      stack = [start_v]
      while stack:
          v = stack.pop()
          if v not in discovered:
                  discovered.append(v)
                  for w in graph[v]:
                      stack.append(w)
      return discovered

• stack: [1] → [2, 3, 4] → [2, 3] → [2, 5] → [2, 6, 7] → ...
• 모든 인접 간선을 추출하고 다시 도착점인 정점을 스택에 삽입하는 구조.

 

너비 우선 탐색(BFS)

시작점에서 가까운 정점들부터 방문하는 방법.

주로 큐로 구현. 그래프의 최단 경로를 구하는 문제(다익스트라 알고리즘) 등에 사용됨.

 

큐를 이용한 BFS

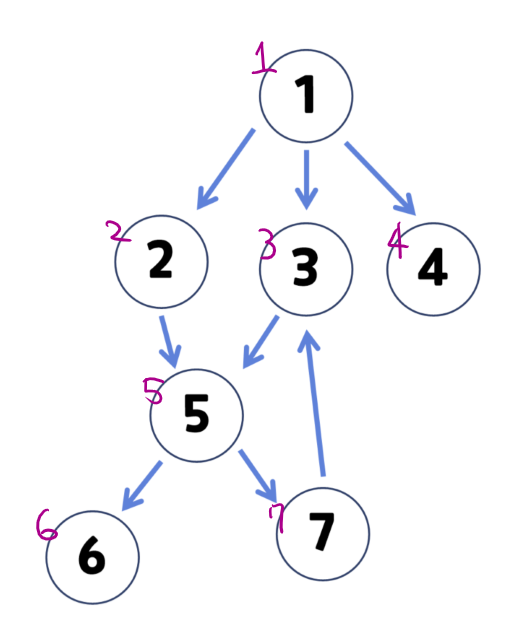
• 큐를 이용한 반복 구조로 구현

  def iterative_bfs(start_v):
  	discovered = [start_v]
  	queue = [start_v]
      while queue:
          v = queue.pop(0)
          	for w in graph[v]:
                  if w not in discovered:
                      discovered.append(w)
                      queue.append(w)
  	return discovered

• discovered: [1, 2, 3, 4, 5, 6, 7]
• queue: [1] → [2, 3, 4] → [3, 4, 5] → [4, 5] → [5] → [6, 7] → [7] → []
• 모든 인접 간선을 추출하고 도착점인 정점을 큐에 삽입
• 재귀로 구현하는 것은 불가능하다.

백트래킹

해결책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포기해 정답을 찾아가는 범용적인 알고리즘

제약 충족 문제에 특히 유용함.

운이 좋으면 시행착오를 덜 거치고 목적지에 도착할 수 있지만, 최악의 경우에는 모든 경우를 다 거친 다음에 도착할 수 있다는 점에서 브루트 포스와 유사.

가지치기(pruning): 큰 트리가 있을 때, DFS로 탐색을 시도한 후 가능성이 없는 후보는 즉시 포기

제약 충족 문제

수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제

백트래킹의 가지치기는 제약 충족 문제를 최적화한다